管楽器でこそ和音を楽しめる！

こんにちは！なつけんです。
大人になってから、サックスを始めて10年近く経ちました。サックスを始めてから、5年ほど経った頃から、吹奏楽団に所属したりと、最初の頃からは考えられないほど、今ではすっかり音楽ライフを満喫しています。

ところで、皆様は管楽器でこそ真の和音を楽しめる、ということをご存知でしょうか？和音というと、「ドミソ」や「ファラド」ですね。

これらはもちろんピアノやギターでも和音を作ることは可能ですが、実は管楽器でこそ真の和音を作れるんです。また、それこそが管楽器の難しいところであり、醍醐味でもあります。

今回は、大人から楽器演奏を始めた人でも真の和音を作る方法、なぜ、ピアノではできないのに、管楽器ではできるのかについて解説します。

純正律と平均律

音階には音と音の高さの間隔によって色んな〇〇律というのが存在します。その中でも最も綺麗な和音が作れる純正律とつか勝手のよい平均律について紹介します。

純正律とは

純正律とは自然倍音を使った音階のことを指します。自然倍音というと難しですが、基準音と綺麗な整数比で表される音のことです。

下にドの音を基準として、純正律におけるそれぞれの音の周波数倍率（ドの何倍の音の高さか）を示しています。
五線譜の下のドから次の1オクターブ上のドまで移ると、音の高さは2倍になるので、分かりやすいですね。

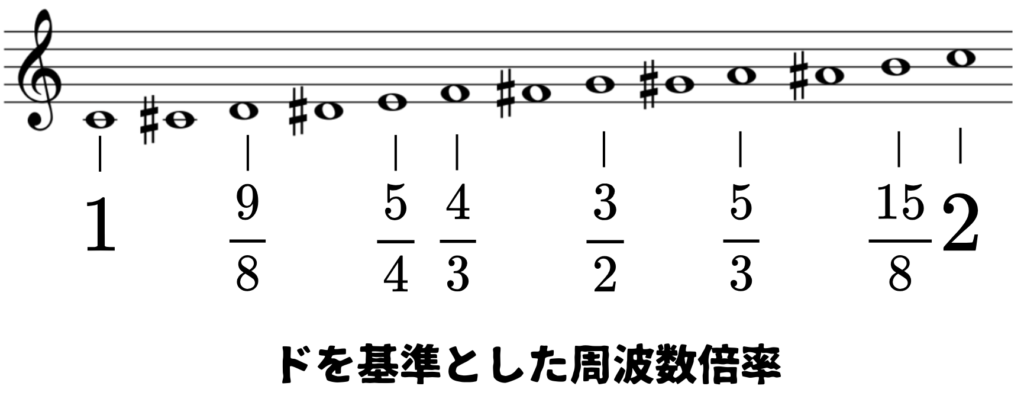
和音の話で言うと、1番分かりやすいのは3和音で「ドミソ」ですね。
「ドミソ」をこのドを基準とした周波数倍率で表すと、\(1:\frac{5}{4}:\frac{3}{2}\)となります。全部に4をかけると4:5:6と綺麗な比になります。

こういった綺麗な比率になる音のみで構成された音階を純正律と言うんですね。

完全に綺麗な和音を作れるのが純正律。しかし欠点もあります。それは転調すると正しい音階にならなくなると言うことです。

それは、純正律は、音階上での音と音の間隔が均等ではいために起こります。例えば、「ドーレ」の全音は周波数比\(8:9\)、「レーミ」の全音は周波数比\(9:10\)で、同一ではありません。

なので、ドを基準とした音階から、レを基準とした音階に転調するとメチャクチャになります。つまり、純正律はめちゃくちゃ綺麗だけど、転調できないという機能欠陥があります。

平均律

そこで、ピアノなどの、音の高さ（周波数）を一度決めたら中々変えることはできない楽器では、自由に転調するために、平均律というシステムが採用されています。

下の絵は平均律の周波数間隔を示しています。1オクターブ上がると周波数が2倍になることは純正律と同じですが、このオクターブを12等分して半音を決めています。

ポイントは12分割を差を12等分ではなく、比を12等分していることです。なので、全ての全音と半音の周波数比は同じになります。例えば、ド→ド＃の比は\(2^\frac{1}{12}\)(2の12分の1乗)であり、ド＃→レの比も\(2^\frac{1}{12}\)となっており、比率は等間隔です。

この平均律によって、転調が可能となる一方で、完全な和音を作ることは難しくなるという欠点があります。

例えば、ドミソで話をすると、ミとソはそれぞれドから半音4つと7つ分移動した音なので、その周波数比率は\(1:2^\frac{4}{12}:2^\frac{7}{12}=1:1.2599:1.4983\)となります。これは純正律で作られたドミソの比4:5:6と比べるとあまりスッキリしないですね。

なので、平均律で作られた和音は大体合ってるけど、純正律で作られた和音には及ばない、となります。

セントという音の高さの単位

では、純正律と平均律はどれくらいズレているのか？を示すことができる単位があり、セントと言います。1セント、2セント・・・と数えます。

セントとは、一体どういう音の単位なのかについて、簡単に説明しますね。
セントは下の絵で示すように、平均律の半音階の半音を100分割したもので、１オクターブ（例えばドから次のド）離れると音の高さは1200セント違うということになります。

上で述べたように、平均律と純正律は音の間隔が異なります。じゃあ一体どれくらい違うの？という時にこのセントで平均律と純正律の差を表すことができます。

実際にはlogという対数を用いて計算するのですが、難しい計算は後にして、基準音（根音）に対する各音のズレ量は下のようになります。

基準音	各音の純正律からのズレ（セント）
	C	C#	D	E♭	E	F	F#	G	A♭	A	B♭	B
C	0	11.7	3.9	15.6	-13.7	-2.0	-9.8	2.0	13.7	-15.6	17.9	-11.7

上の表ではわかりやすく、基準音をCとした時の純正律からのズレを示しています。この表だけだとイマイチピンとこないですが、平均律と純正律を絵で表すと下のようになります。

基準音をドとした時に純正律のミの音の高さは平均律のミよりも13.7セント低いし、純正律のソの音の高さは平均律のソよりも2.0セント高いということが分かります。

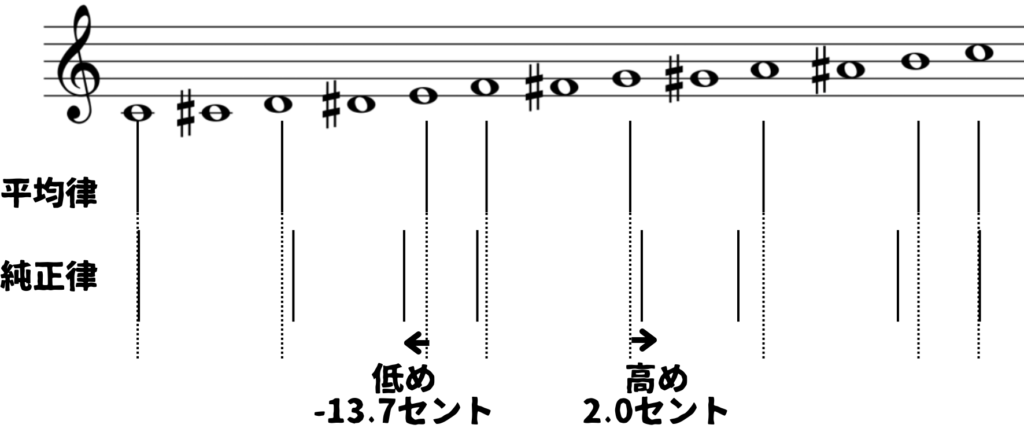
が、基準音が変わっても、基準音から半音が何個分違うかを見れば、純正律からのズレ量は同じになります。

例えば、基準音がF（ファ）の場合、半音４つ異なるのは、A（ラ）ですね。この時、Aの純正律と平均律のズレ量は上の表のCとEの関係である-13.7となります。

具体的にどうすればいいか

ここまでの話から純正律と平均律の音の高さは少し違う。完璧に綺麗な和音を作りたければ純正律の音の高さにしないといけない。ということが分かりました。

では、綺麗な純正律の和音を作るためには、具体的にどうすればいいのか。

答えは簡単で、（やるのは難しいですが）管楽器を使うことです。

ピアノやギターは一旦調整するとピッチが固定されていますね。ところが管楽器だと、息の入れ方や口の使い方で多少の音程の上下が可能となります。

トロンボーンとかで考えるとわかりやすいですね。トロンボーンは管のスライドで無限に細かく音を上下できます。サックスも息の入れ方で音程は変わりますね。

つまり、その都度、出したい和音やその時の役割によって音程を少しコントロールして純正律の綺麗な比率の和音を作るわけです。

一番基本となる和音である3和音で話します。ここでは例としてドミソで話します。
この場合、基準となる音はドで、ミは平均律より13.7セント低く、ソは平均律よりも2.0セント高い音を出す必要があります。

身もふたもない話ですが、はっきり言って、大人初心者にとって、2.0セントの違いは難しいです。だって、半音の100分の２の違いですからね。

でも、13.7セントは目で確認できます！

下の写真はよくあるヤマハのチューナーですが、画面をよく見ると、左下と右下に「CENT」の文字があることが分かります。チューナーの針は真ん中がピッタリ音程が合うのはもちろんですが、実は音程のずれはセント単位で表示してくれています。

チューナーには真ん中の左右に逆三角形が表示されています。実はこの三角は純正律のピッチの目安を示しています。また、よくよく見ると、左右の三角の中央からの距離は対称では無いですね。

左の三角は-13.7セントを示していて、右の三角は15.6セントを示しています。
左の三角はメジャーコード（長調）の”ドミソ”で”ミ”を担当する時に指標になりますし、右の三角はマイナーコード（短調）の”ドミ♭ソ”で”ミ♭”を担当する時に音の高さの指標となります。

実際に練習する時、例えばドミソの和音の中で”ミ”を担当する時には、下の写真のように、-13.7セントの高さにあわせます。つまり、チューナーを見ながら息の入れ方や、口のアンブシュアの感覚を覚えると綺麗な和音を作れるようになります。

まとめ

今回は、管楽器でこそ作れる真の和音について解説しました。内容を以下にまとめます。

参考になれば嬉しいです。

以上、なつけんでした。

おまけ：セント差を計算するとどうなるか

ここからは「セントは一体どうやって計算しているのか」気になる人向けです。

上で、セント数の差の表を出しました。このセント数-13.7や15.6はどうやって出すんでしょう？
ここではおまけで、計算での出し方について解説します。使うのは高校数学で習う指数・対数というものです。

まず、「ミの純正律と平均律の差は-13.7」を計算してみます。下記の３つから計算します。

• 平均律では半音の間隔を100セント→ドとミは半音4つなので400セント離れている
• ドから１オクターブ上のドは音の高さは2倍違い、セントで言うと1200セント離れている
• 純正律ではミの音の高さはドの\(\frac{5}{4}\)倍

上で書いてることの繰り返しですが、セントという単位は半音の間隔を100セントとする、でしたね。今、求めたいのは純正律でドとミが何セント離れているか？なので、これを\(x\)とします。

以上から、ミの音の高さを指数を用いると、\(2^{\frac{x}{1200}}\)と表せます。仮に\x=1200\とすると、\(2^{\frac{x}{1200}}=2^{\frac{1200}{1200}}=2^{1}=2\)となり、１オクターブ上のドを表します。

一方、純正律のミ音はドの\(\frac{5}{4}\)倍なので、これら２つの式はイコールとなり、下のような方程式を解いていきます。

$$2^{\frac{x}{1200}}=\frac{5}{4}$$

両辺を対数にして、

$$log_{10}{2^{\frac{x}{1200}}}=log_{10}{\frac{5}{4}}$$

$$\frac{x}{1200} \times log_{10}{2}=log_{10}{5}-log_{10}{4}$$

$$x=1200 \times \frac{log_{10}{5}-log_{10}{4}}{log_{10}{2}}$$

$$x=1200 \times \frac{0.69897-0.60206}{0.30103}=1200 \times 0.32193=386.316$$

以上の計算により、純正律のドとミは386.316セント離れていることがわかりました。平均律の400セントとの差は13.684で、およそ13.7違うことがわかります。

その他の音に対しても同様に、基準となるドの（純正律で）何倍の高さかと、ドから何セント離れているかを計算することで、平均律と純正律のズレを計算することができます。